Welcome to my little corner of the datacratic blog where I'll be writting about random bits of interesting code that I happen to be working on at the moment. I'll start things off by describing a fun little algorithm that I recently wrestled with, namely, a 3-way trie merge.
These last few months, I’ve been building a soon to be open-sourced in-memory database capable of filling the needs of our real-time machine learning platform. It uses a trie that loosely resembles a Judy array1 as its primary storage data structure and it was designed to handle thousands of concurrent reads and writes in real-time. While reads to the trie were easily scalable, the writes were not doing so well and a bit of profiling revealed that our MVCC scheme created a bottleneck at the root of the trie which had the effect of serializing all the writes. After several failed attempts to tweak and prod the scheme, it became apparent that the problem had to be tackled from another angle.
Before we go any further let's take a quick refresher on the different types of merges using git as an example.
- A 2-way merge is the equivalent of a git fast-forward: if we attempt to merge a branch A into a branch B where no new commits were added since we forked branch A, then git will simply redirect branch pointer B to to the head of branch A.
- A 3-way merge is simply merging a branch A into a branch B where one or more commit was added since we forked branch A. This will cause git to generate a merge commit with both the modifications of A and B. Note that, occasionally, a modification in B will conflict with a modification in A and git will prompt the user to resolve the conflict.
- A N-way merge can be thought of as a series of 3-way merges. In git terms, if we have branches A, B and C that we want to merge into master then we would first merge A then B then C in three separate operations.
So how do we make writes scalable with a 3-way merge? We first need to get around the MVCC bottleneck by forking the trie into isolated transactions where several modifications can grouped together2. Now that concurrent modifications can't affect each other, we can run several transactions in parallel to achieve our goal of scaling writes. That's great but the writes are still isolated and only visible to the current thread which is not all that useful. To make them globally visible we'll have to commit the changes back into the main trie using a merging algorithm. While we would like to use with a simple 2-way merge algorithm, it limits us to a single live transactions so we have to implement the more complicated 3-way merge algorithm.
Terminology
In this section we'll define a few terms that will be use throughout the article. First up, we’ll associate a label to each of the 3 trie versions we’re going to manipulate:
![]()
- base: The version of the trie where the fork took place.
- dest: The current version of the trie that we want to merge into. This may point to the same version as base in which case we’re dealing with a 2-way merge.
- src: The local version which contains our modifications that we want to merge into dest.
Next, we'll describe a trie representation that the algorithm will work on. We could pick any one of the many trie variants but that would require that we worry too much about implementation details. Instead we'll use a simplified representation that should translate easily to any trie variants. This is what a single node will looks like:
![]()
To start off, our representation uses a binary tree which implies that we'll manipulate our keys as bits instead of bytes. While this simplification will greatly facilitate the comparison of nodes, it still has a considerable impact on the depth of the trie. The good news is that extending the representation and the algorithm to an n-ary alphabet is relatively straight-forward.
The solid vertical lines are used to represent fragments of keys where the length of the line represents the number of bits contained within that key fragment. As an example, the line labelled prefix is a bit string that prefixes all the keys that can be reached from the current node. Alternatively, it's the path from the root to our current node.
The beginning of a node is marked by a circle and the node itself can be composed of a value and two child nodes which all share a common key fragment prefix. The fragment of that common prefix that is not shared with the node's prefix is called the common suffix. As an example, the key associated with the node's value is the node's prefix concatenated to the node's common suffix. Similarly, the key associated with a node's child is the node's prefix concatenated with the node's common suffix and an additional bit for the branch illustrated by the diagonal lines. As a convention, the left and right branches will represent bit 0 and 1 respectively which ensures that a preorder traversal of the tree will yield the keys in a lexical order.
The branching point represents the bit position where the common suffix of two different nodes differ from each other. This will be used to compare the content of two nodes and it will be properly introduced a bit later.
Running Example
We have one last hoop to jump through before we get to the fun stuff. Below is an example that we'll use for the rest of the article to make algorithm a bit more concrete.
![]()
Here we have the three versions of a trie that we will merge into the final trie at the bottom. The trie starts off as base with the key-value pair (0101, a) and (0101100, b). To get src, we first fork base then we remove (0101100, b) and insert (0101011, c). Meanwhile, (010101100, d) is inserted into base to form dest. We then want to merge src back into base which, if done successfully, will result in the final trie that contains the following key-value pairs:
(0101, a) which was never modified,(0101011, c) and (010101100, d) which were inserted into src and dest respectively,- but not the
(0101100, b) which was removed from src.
It's worth noting that if we were to use either src or dest as the final trie version then we would discard changes made in the other version. Also, if we were to use dest and src without base to do the merge, we would be unable to decide what to do about the (0101100, b): was it added in dest or removed in src? This is why we need a third version that gives us a point of reference to resolve ambiguities. In other words, that's why we need to do a 3-way merge instead of a simple 2-way merge.
Generic Algorithm
In my first attempts at writing this algorithm, I quickly realized that trying to handle all three trie versions at once would get complicated fast. Not only was it difficult to handle all the scenarios cleanly, the code for walking and comparing the trie versions also ended up being scattered throughout the algorithm. It was a mess.
To avoid all these problems, we need a more unified framework for walking and comparing tries. We can start by dividing the problem into three phases:
- diff: search for differences between the base and src tries. When a difference is spotted, it delegates the modifications to the insert or remove phase.
- remove: remove a subtree of the base trie from the dest trie.
- insert: insert a subtree of the src trie into the dest trie.
These phases boil down to looking for changes between base and src and applying them to dest as appropriate. In our running example this corresponds to finding the src operations insert (0101011, c) and remove (0101100, b) which are then applied to dest to form the final trie. Note that this would work equally well if we were to find dest's insert (010101100, d) operation and apply it to src. While dividing the problem this way is quite intuitive, the real gain is that all three phases only need to manipulate two out of three versions to do their work. This will greatly simplify the number of cases we have to worry about when merging.
Now that we’ve reduced the problem, we need a way to walk a pair of tries in a synchronized fashion while looking out for differences. This can be accomplished using a surprisingly powerful generic algorithm which will form the core of each phases. Here’s a lightly simplified version of the code:
void merge(const Cursor& c0, const Cursor& c1)
{
// Figure out where the next difference occurs.
uint32_t bitNum = commonPrefixLen(
c0.prefix() + c0.commonSuffix(),
c1.prefix() + c1.commonSuffix());
// Parse the content of the nodes
BranchingPoint p0(c0, bitNum);
BranchingPoint p1(c1, bitNum);
bool doMerge = false;
// Compare the nodes' branches
for (int branch = 0; branch < 2; ++branch) {
if (!p0.hasBranch(branch) && !p1.hasBranch(branch))
continue;
if (!p0.hasBranch(branch) || !p1.hasBranch(branch)) {
doMerge = true;
continue;
}
// Both branches are present.
Cursor newC0 = c0.advanceToBranch(p0, branch);
Cursor newC1 = c1.advanceToBranch(p1, branch);
merge(newC0, newC1);
}
// Compare the nodes' values
if (p0.hasValue() || p1.hasValue())
doMerge = true;
// Merge if necessary
if (doMerge)
mergeBranchingPoints(c0, p0, c1, p1);
}This code sample makes heavy use of two utility classes: Cursor and BranchingPoint. Cursor allows us to easily move around the trie via the advanceToBranch function while keeping track of which node we’re currently looking at along with its prefix and its common suffix. BranchingPoint is used to parse the content of a node by grouping its elements into branches for the given bit number. As an example:
![]()
Constructing a BranchingPoint on this node at the 8th bit will group all three elements A, B and C on the same branch. If we use the 16th bit instead, then A will be on branch 0, B on branch 1, and C will be tagged as a value. This abstraction makes it dead easy to compare the content of any two node no matter where we are within its common suffix.
Now that the details are out of the way, we can look at the algorithm itself. Its input consists of two cursors that initially points to the root nodes of any two trie versions. It starts by comparing the prefix and common suffix of both cursors to determine where they first differ. It then constructs a pair of BranchingPoint at the first difference and uses them to figure out how the merge should proceed.
If a branch is missing in one trie and present in the other then we know there is a problem and we ask the current phase to take an action via the mergeBranchingPoint function. If a branch is present in both nodes, then we recursively invoke merge on that branch in both tries. Notice that when we do a recursive call, both branches have identical prefixes. This guarantees that we always make progress down the trie because the branching point of the callee will always have branching point with a bit position greater then the branching point of the caller.
Finally, we’ll see later that the rules surrounding values differ in all three phases. This forces the generic algorithm to always call mergeBranchingPoint if a value is present in either tries.
In a nutshell, the generic algorithm does a depth-first walk of a pair of tries and triggers a callback whenever it spots a difference between the two. The rest of the article will detail how each of the three phases implement the mergeBranchingPoint function to achieve a 3-way merge.
Diff Phase
The neat thing about the generic algorithm of the previous section is that it does almost all of our diff-ing work for free. To see how, let’s diff the following two nodes:
![]()
When the generic algorithm evaluates the indicated branching points, it will find that the branch A in base is not present in src. This is due to the user removing the values of the A subtree from the src trie. Similarly, it’ll notice that there is the branch B in src that is not present in base. This is due to the user adding values to the src trie that were not present in the base trie. In both cases, the generic algorithm will ask the current phase to take an action. For diff-ing this consists of comparing the given BranchingPoint objects and switching to the insert or remove phase as appropriate. That’s it!
In all three phases we can take a shortcut if, in our trie implementation, we can tell whether a subtree has been modified by only looking at the root of that subtree. For diff-ing, it can be used to prune a subtree if src was not modified and is therefore identical to the equivalent base subtree. We can also tell when we’re dealing with a 2-way merge if there are no modifications in dest. If this is the case, we know that the dest subtree is identical to the base subtree and we can merge the src subtree by swapping it with the dest subtree.
In general, we’re able to exploit 2-way merges in all three phases and it will have a dramatic impact on the performance of the algorithm. The gains come from the ability to merge an entire subtree without having to explore it. As an example, let's partition the key space manipulated by each forked version of the trie so that there's very little overlap between the modified subtrees of each versions. As a result, the merge will find many 2-way merge opportunities near the top of the tree and will be able to avoid visiting the majority of the tree's node which reside at the bottom of the tree.
Now let's take a look at our running example to see how the diff phase behaves there.
![]()
The first branching point raised by the generic algorithm will be at the key prefix 0101 because of the branch mismatch in the root node: base's branch 1 is not present in src and src's branch 0 is not present in base. As we've seen earlier, the diff phase will invoke the remove phase on base's branch 1 which should remove the key-value pair (0101100, b). It will also invoke the insert phase on branch 0 which should insert the key-value pair (0101011, c).
Remove Phase
In this phase we’re trying to remove a base subtree from dest. It turns out that there's very little we need to do here beyond walking down the trie which is conveniently handled by our generic algorithm. Take the following two subtrees as an example:
![]()
Here we would like to remove all the values in the subtree A from the dest subtree. The problem is that another merge already beat us to it so there is very little we can do. In general, we never have to look at the branches because the only relevant scenario is if both branches are present. In this case we need to dig deeper into those branches to make sure we don’t delete values that were added to dest after the fork. It so happens that this is handled transparently by the generic algorithm so we can just ignore branches.
All we’re left with are the values B and C which can conflict with each other. If B is equal to C then we can safely remove C from dest because the value we want to delete wasn’t changed by another merge3. If B is not equal to C then we have two competing modifications of the same key and we need to decide which one will make it to the final trie. Since there is no realistic way to divine the intent of the user, we just trigger a callback and let someone else deal with the mess.
Another reason to use callbacks to resolve conflicts is that it opens up interesting merging behaviours for the users. As an example, if the trie's values represent lists then we can resolve a remove conflict by only removing the elements in the base list that are present in the dest list. This would preserve any elements that were added to the list after the fork took place.
Finally, if we’re in a 2-way merge then we can just get rid of the entire dest subtree because it’s the base subtree we’re trying to remove.
Before we move on to the insert phase, let's get back to our running example and see how the remove phase behaves when trying to remove the branch we identified during the diff phase.
![]()
There's two way this phase can proceed: with or without a 2-way merge. If we're allowed to use 2-way merges then we'll notice that no modifications have taken place in branch 1 of dest which allows us to just remove the entire subtree. If we can't make use of 2-way merges, the generic algorithm will keep digging until it reaches the illustrated branching point. We then need to compare the values directly and check for conflicts. Since we didn't modify the key 0101100 in dest, there is no conflict and we can just remove dest's value.
Once the value is removed, we'll be left with a dangling node that doesn't point to anything. Ideally we would also get rid of that empty node so that we end up with the clean trie illustrated on the right but it turns out that simplifying nodes can get pretty tricky and will depend on the trie implementation. We'll tackle this problem in a follow-up article
Insert Phase
In this phase, we’re trying to insert a src subtree into dest. The simplest approach is to walk the src subtree and gather all its values which we would then insert one by one into the dest subtree. Unfortunately for our trie implementation and for most trie variants, this is not very efficient because it requires that we do many successive modifications to the dest trie. What we really want is to look for situations where we can directly insert an entire subtree of src into dest because moving an entire subtree can be implemented by simply redirecting a pointer. There's two scenarios where we can take this shortcut.
The first occurs when the branching point is at the end of the dest’s common suffix and if we have a branch in src but not in dest.
![]()
As the above trie diagram illustrates, there is already an empty branch in the C node where we can conveniently insert A after trimming its common suffix. Nice and simple.
Things get a little bit more tricky if the branching point is within the common suffix of a dest node.
![]()
Here we have no empty branch we can use, so instead we’ll create an entirely new node E with one branch going to the src node A and the other going to the dest node C. We also need to trim the common suffix of A and C so that they only contain the portion below the branching point. Because E will be inserted into dest, its common suffix will become the fragment of C's common suffix which is above the branching point.
Depending on the trie variant, this may or may not take care of all the possible scenarios. The fallback is to start inserting values manually which can lead to conflicts. Let’s say we have a src value A and a dest value B. If A and B are equal then we don’t need to insert anything because another merge beat us to it. If A and B are not equal then we have a problem: we can’t tell if we have a conflict without looking at base to see if dest’s value was changed after the fork. This can be solved by either always raising a conflict or updating the base cursor as we’re walking down src and dest4.
Finally, if we’re in a 2-way merge scenario then we can just swap the dest subtree with the src subtree.
Let's take one final look at our running example to see how the insert phase behaves when we try to insert the branch we identified during the diff phase. Note that we've already executed the remove phase so dest's branch 1 was already removed.
![]()
To start, the generic algorithm will walk down the branch until it reaches the illustrated branching point which occurs in the middle of dest's common suffix. This means that we're in the second scenario and we need to create a new node to break up dest's common suffix. We then insert the src branch, which is composed of only a single value, into the new node. Once that's completed, we're left with the final trie we were looking for so we're done!
Not quite done yet...
While I would like to say that this is all you need to implement your own 3-way trie merge algorithm, the reality is that I've deliberately omitted several thorny implementation details. There's a whole lot more to be said about garbage collection, node simplification and n-ary alphabets which are all a great source of mind-bending bugs. Before I can dig into implementation details, we'll need an actual trie implementation which I'll introduce in a follow-up article. Eventually, I'll get around to writing about the performance characteristics of the algorithm and whether we can improve them through parallelization.
1. While we reuse some basic ideas, our trie variant has some fundamental differences with Judy arrays. We'll take a closer look at our trie implementation in a follow-up article.
2. Coincidentally this gives us the A, C and I letters of ACID. While we could also get the D, our snapshotting mechanism is simply not optimized for this use case and would considerably slow down any commits. More on snapshotting at some point in the future.
3. This is not entirely true. As an example, if the value is a pointer to a mutable structure then the algorithm has no way of knowing if the structure has been modified or not. This can be solved by only allowing immutable values into the trie.
4. In our trie variant, we already needed to update the base cursor to detect 2-way merge scenarios so this decision was a no-brainer.



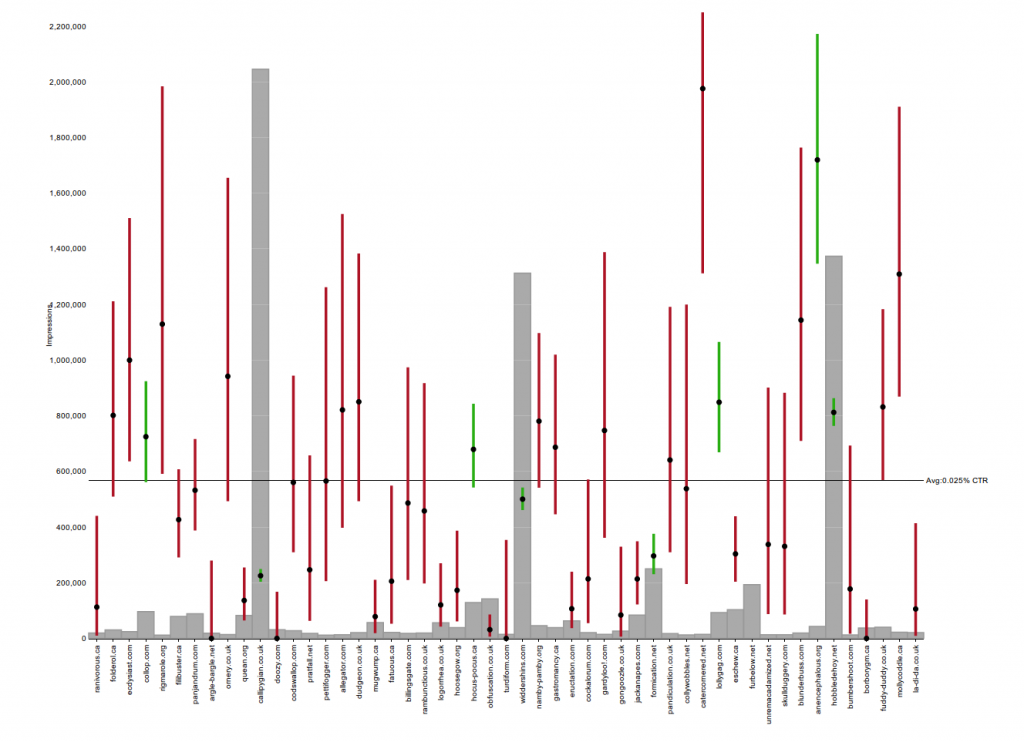
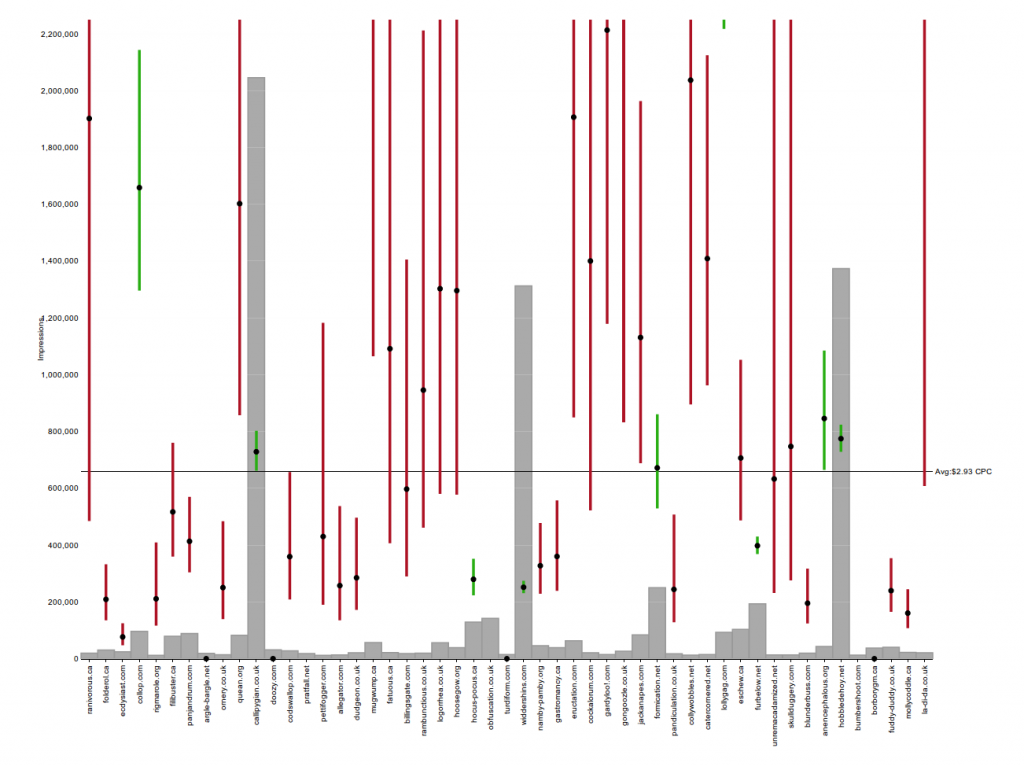
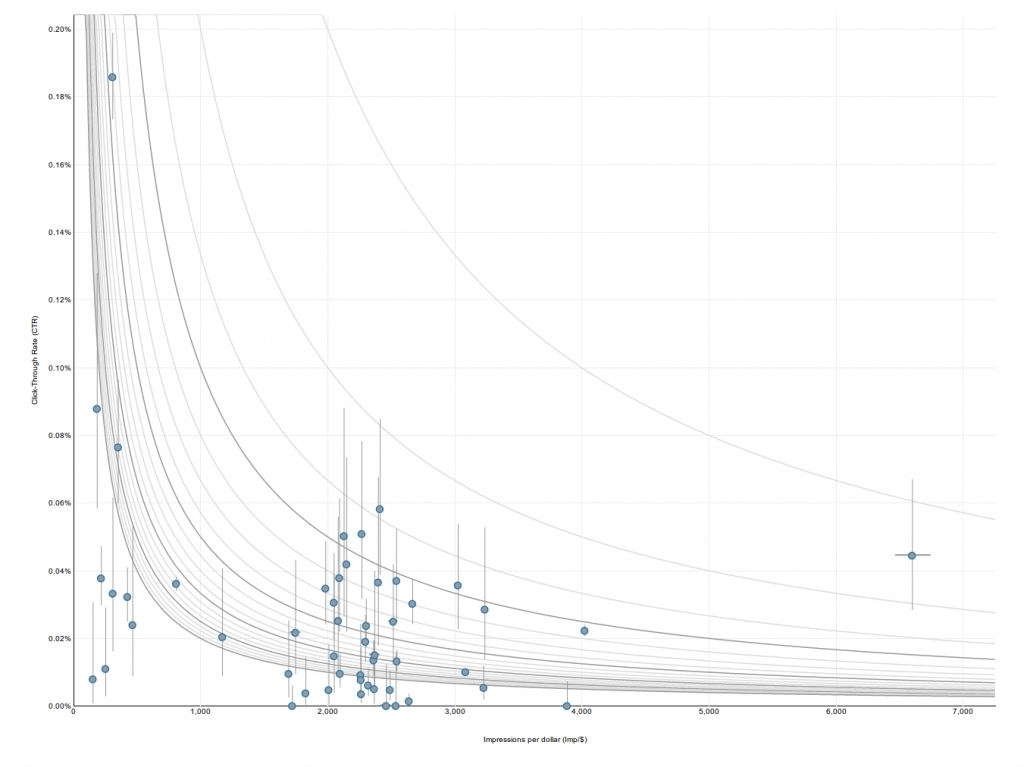


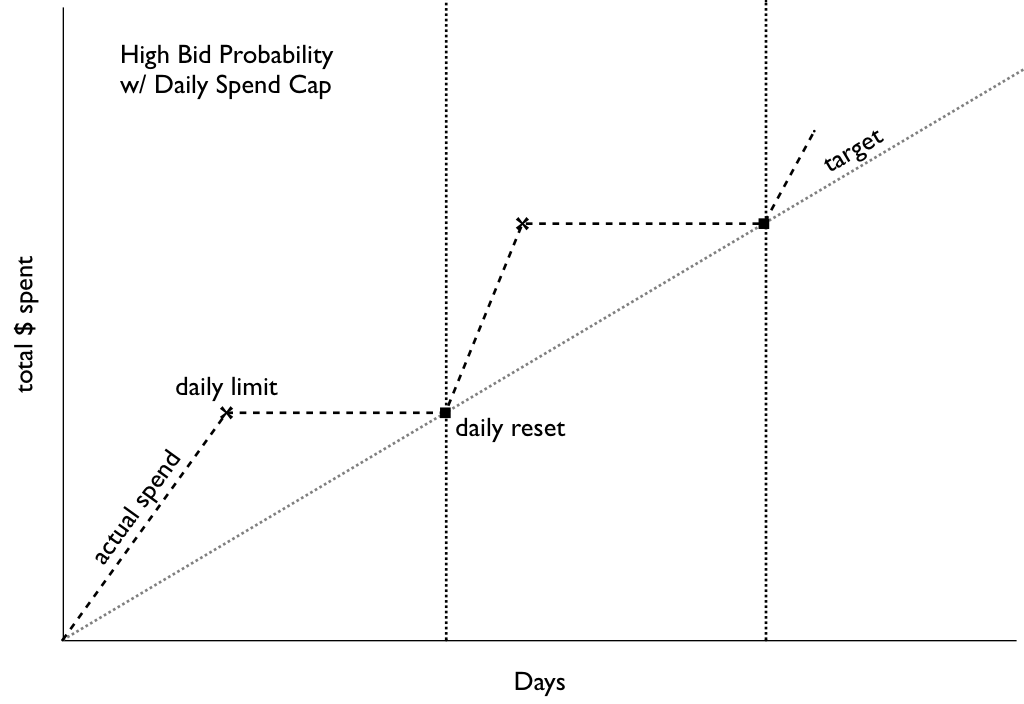
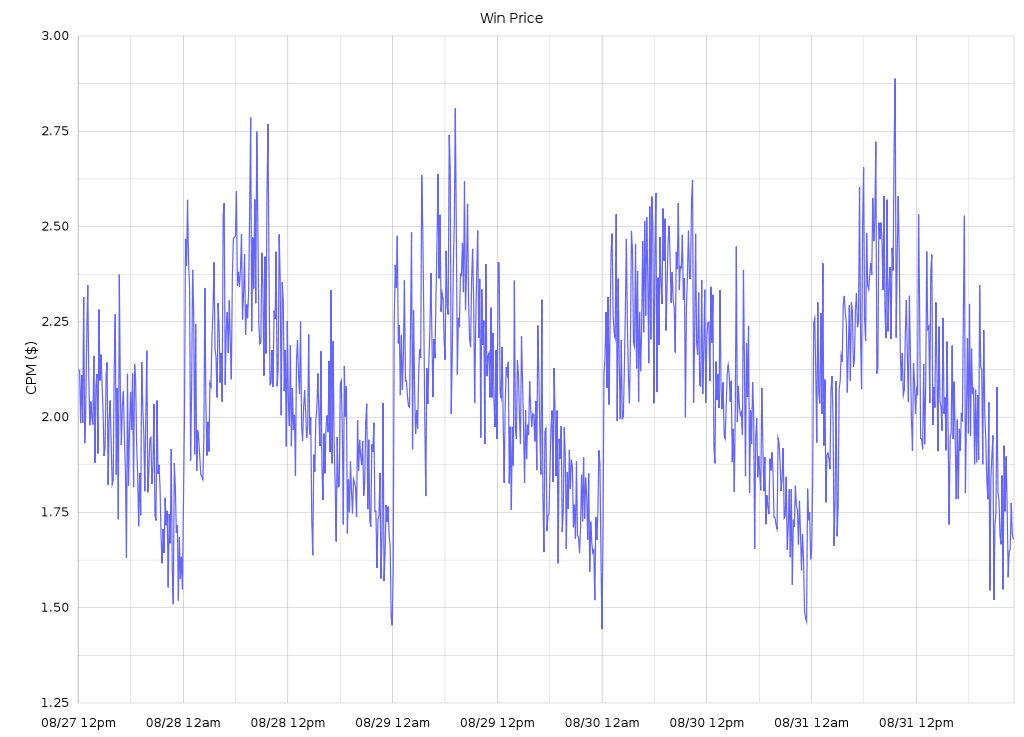
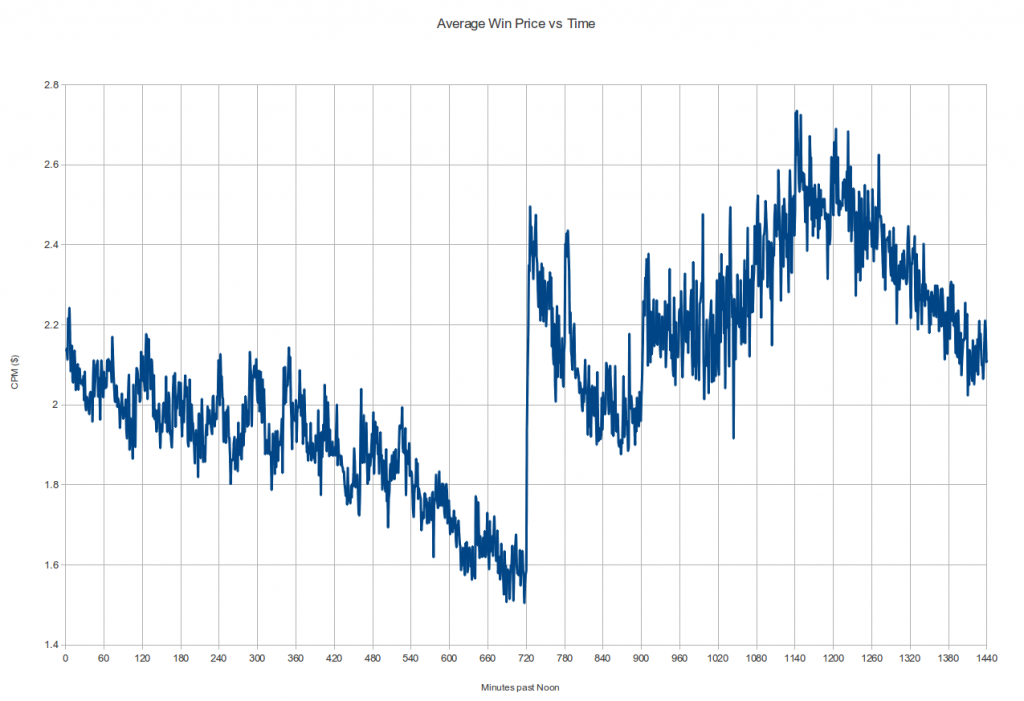
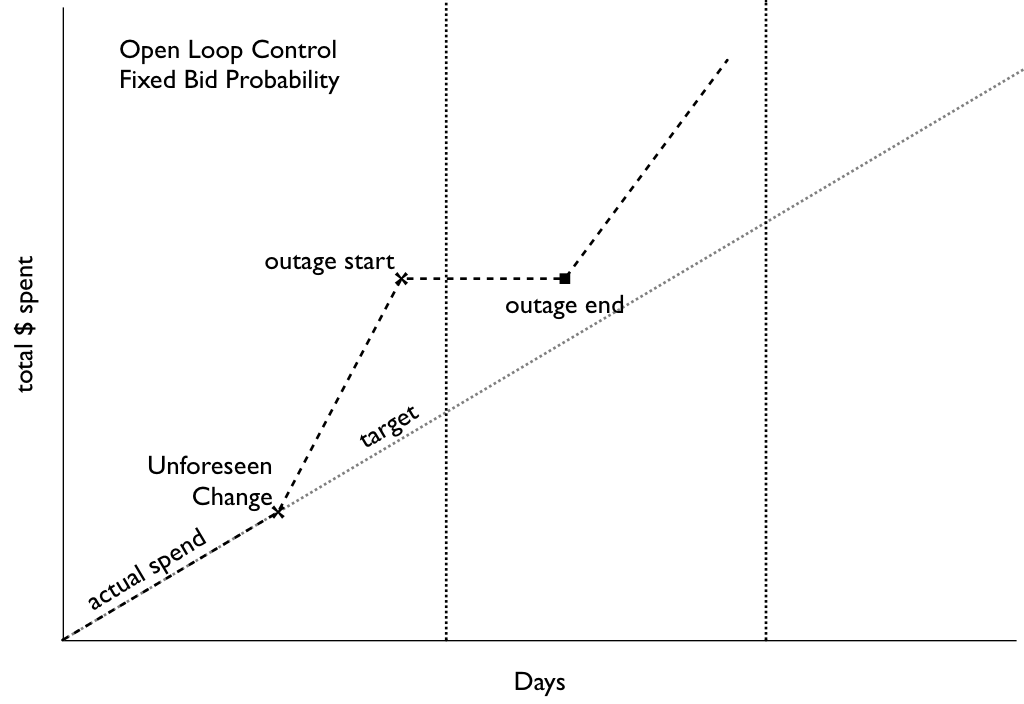
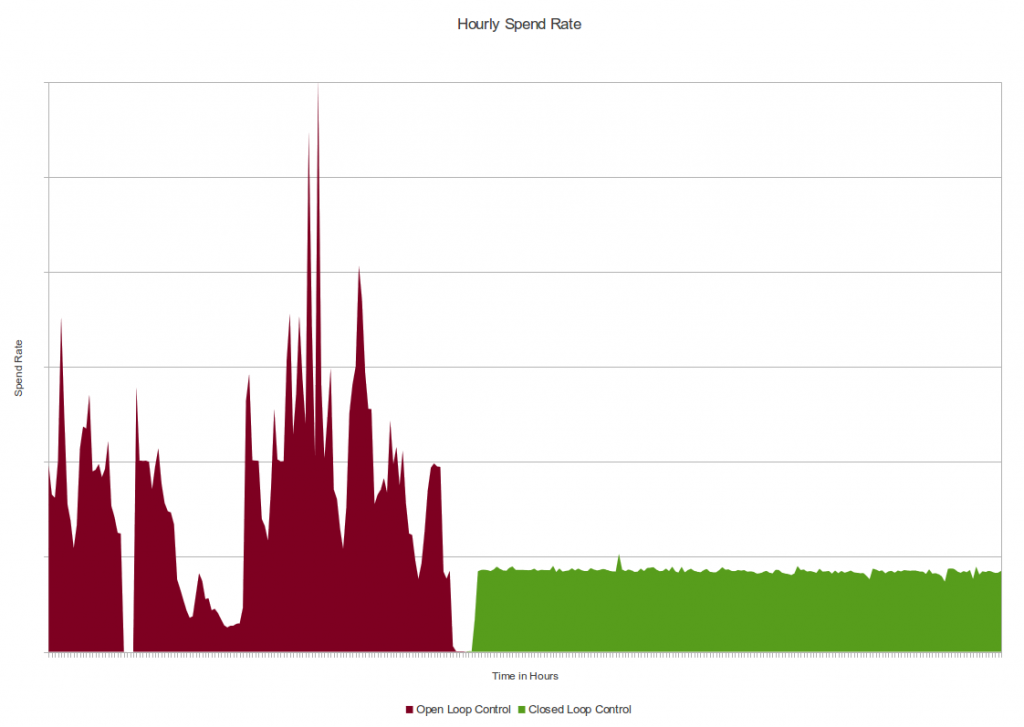














 In this CTR quantile plot of sites for an actual campaign, the vast majority of sites aren't much more than 1 standard deviation away from the mean. The exceptions are the sites with extremely high CTRs in yellow and red at the top.
In this CTR quantile plot of sites for an actual campaign, the vast majority of sites aren't much more than 1 standard deviation away from the mean. The exceptions are the sites with extremely high CTRs in yellow and red at the top. Screenshots of sites caught by the Too Good To Be True filter at around the same time
Screenshots of sites caught by the Too Good To Be True filter at around the same time











